El Círculo Trigonométrico, también conocido como círculo goniométrico, es aquel círculo cuyo centro coincide con el origen de coordenadas del plano cartesiano y cuyo radio mide la unidad (r = 1). El círculo trigonométrico es una herramienta práctica y un apoyo teórico fundamental, ya que ayuda a fundamentar y obtener una idea precisa y formal de las funciones trigonométricas. A través del círculo trigonométrico se puede obtener de forma manual o analítica el valor aproximado de las razones trigonométricas para un ángulo determinado si se dispone de los instrumentos geométricos necesarios.
Sumario
Características
Se toma como base un círculo de radio r = 1 con centro O, en el origen del plano cartesiano. Se considera un ángulo arbitrario medido a partir del eje x positivo y en sentido positivo; es decir, en sentido contrario a las manecillas del reloj. Todo ángulo puede ser colocado (y de una sola manera) de forma tal que su vértice coincida con el origen de coordenadas, uno de sus lados (llamado lado inicial) coincida con la semirrecta OA y el otro lado (llamado lado terminal) quede ubicado (a partir del inicial) en la zona de barrida en sentido contrario a las manecillas del reloj.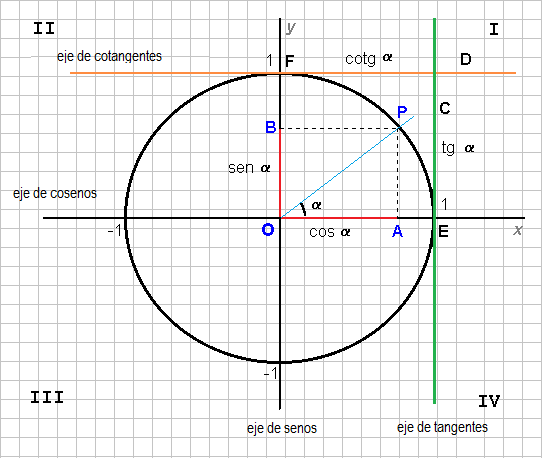
Si la semirrecta r = 1 la hacemos rotar en sentido contrario a las manecillas del reloj, describe un círculo dividido en 4 cuadrantes (I, II, III, IV). Antes de que la semirrecta OP comience a rotar, coincide con el rayo OA, formando un ángulo de 0°. Cuando la semirrecta OP rota, describe un ángulo α, el cual alcanza su máximo (describiendo un círculo completo) a 360° (2π medido en radianes). De esta forma, el lado terminal de cada ángulo interseca en un único punto a la circunferencia y podemos asociar el ángulo a ese punto de manera unívoca.
Razones Trigonométricas
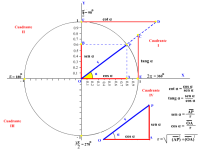
Si la semirrecta OP de radio r rota hasta formar un ángulo α, al proyectar el punto P sobre los ejes X y Y, se obtienen dos segmentos. Sobre el eje Y se proyecta el segmento OB, denominado seno del ángulo α (sen α). Sobre el eje X se proyecta el segmento OA, denominado coseno del ángulo α (cos α). Esto forma un triángulo rectángulo OAP, donde:
- El lado AP se le denomina cateto opuesto al ángulo α.
- El lado OA es el cateto adyacente al ángulo α.
- El lado OP = r se denomina hipotenusa.
Del triángulo rectángulo anterior podemos denotar las razones trigonométricas siguientes:
- sen α = PA/r
- cos α = OA/r
- tan α = PA/OA
- cot α = OA/PA
Seno del ángulo α
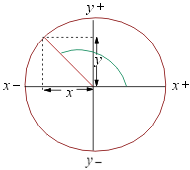
A partir del ángulo α y la semirrecta r se obtiene el punto P. Al trazar una perpendicular desde dicho punto hacia el eje Y, se obtiene un segmento OB = AP que se denomina seno del ángulo α (se denota como sen α). También se determina a través de la razón (PA/r).
Coseno del ángulo α
A partir del ángulo α y la semirrecta r se obtiene el punto P. Al trazar una perpendicular desde dicho punto hasta el eje X, se obtiene un segmento OA = BP que se denomina coseno del ángulo α (se denota como cos α). También se determina a través de la razón OA/r.
Tangente del ángulo α
Si trazamos una semirrecta EC tangente a la circunferencia por el punto E, que toque la semirrecta OD (prolongación de la semirrecta r), se forma el segmento EC que se denomina tangente del ángulo α (se denota como tan α). También se determina a través de la razón PA/OA.
Cotangente del ángulo α
Si trazamos una semirrecta FD, tangente al punto F y que toque la semirrecta OD, se forma un segmento FD denominado cotangente del ángulo α (se denota como cot α). También se determina a través de la razón OA/PA.
Cuadrantes del Círculo Trigonométrico
Si dividimos el círculo trigonométrico en 4 partes iguales, se obtiene como resultado que cada ángulo consecutivo mide 90° (π/2 rd). Cada una de las partes obtenidas se conoce como cuadrantes del círculo trigonométrico. En cada cuadrante, los parámetros seno, coseno, tangente y cotangente cambian su valor numérico con el aumento o disminución del ángulo α, hecho que se corrobora con las razones trigonométricas anteriores.
Primer Cuadrante (0° < α < 90°)
Signos de las Razones
- Seno: +
- Coseno: +
- Tangente: +
- Cotangente: +
En el primer cuadrante (I), con el aumento del ángulo α, disminuyen el cos α y la cot α, mientras que aumentan la tan α y el sen α, hasta alcanzar su máximo o mínimo valor a 90° (π/2).
Segundo Cuadrante (90° < α < 180°)
Signos de las Razones
- Seno: +
- Coseno: –
- Tangente: –
- Cotangente: –
En el segundo cuadrante (II), con el aumento del ángulo α, disminuyen el sen α y el valor absoluto del cos α. Por lo tanto, también disminuyen tan α y cot α, alcanzando su mínimo valor a 180° (π).
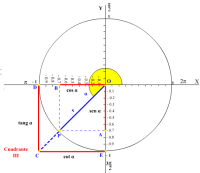
Tercer Cuadrante (180° < α < 270°)
Signos de las Razones
- Seno: –
- Coseno: –
- Tangente: +
- Cotangente: +
En el tercer cuadrante (III), con el aumento del ángulo α, el valor absoluto del sen α y el cos α disminuyen. La tan α aumenta su valor, mientras que la cot α disminuye (dado que el seno y el coseno son negativos y por la relación existente entre ellos) hasta alcanzar su mínimo o máximo valor a 270° (3π/2).
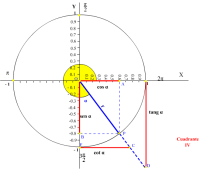
Cuarto Cuadrante (270° < α < 360°)
Signos de las Razones
- Seno: –
- Coseno: +
- Tangente: –
- Cotangente: –
En el cuarto cuadrante (IV), con el aumento del ángulo α, disminuye el valor absoluto del sen α, mientras que aumenta el cos α. Por lo tanto, la cot α aumenta, mientras que la tan α disminuye, hasta alcanzar su máximo y mínimo valor a 360° (2π).
Véase también
Fuente
- LT. Matemática 10mo grado: colectivo de autoras
- dcb.fi-c.unam.mx
- www.educ.fc.ul.pt