Diagrama de Venn: Representación de Conjuntos
Un diagrama de Venn es una representación gráfica que se utiliza para mostrar las relaciones lógicas entre diferentes conjuntos. Fue desarrollado por el matemático John Venn en el siglo XIX.
Características Principales
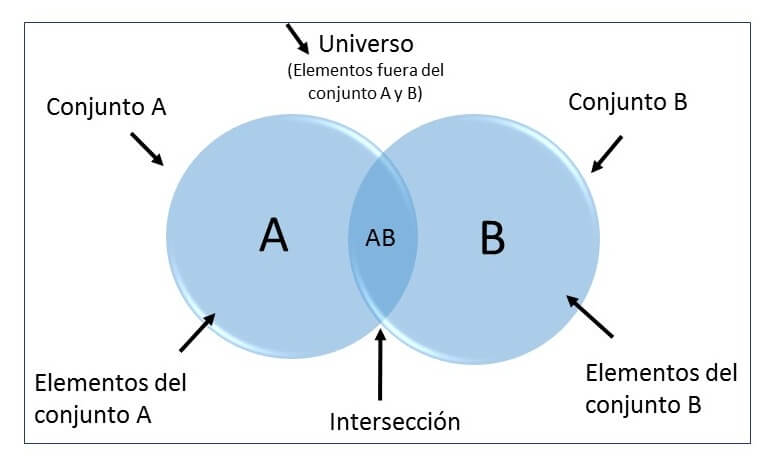
Utiliza círculos superpuestos (u otras formas cerradas) para representar conjuntos.
La intersección de los círculos representa los elementos que son comunes a esos conjuntos.
Las áreas no superpuestas muestran los elementos que pertenecen a un conjunto pero no al otro.
Se puede usar con dos o más conjuntos.
Ejemplo Sencillo
Supón que tenemos dos conjuntos:
Conjunto A: Personas a las que les gusta el helado.
Conjunto B: Personas a las que les gusta el chocolate.
El diagrama de Venn mostraría:
Una parte del círculo A que no se superpone con B: personas que solo gustan del helado.
Una parte del círculo B que no se superpone con A: personas que solo gustan del chocolate.
La intersección entre A y B: personas que gustan de ambos.
Usos Comunes del Diagrama de Venn
Matemáticas (teoría de conjuntos)
Lógica
Estadística
Resolución de problemas
Comparación de conceptos o ideas en educación
Representación Visual
Razones Matemáticas: Comparación de Cantidades
En matemáticas, una razón es una forma de comparar dos cantidades mediante una división. Expresa cuántas veces una cantidad contiene a otra o la relación proporcional entre dos valores.
Definición de Razón
Una razón es el cociente de dos números.
Por ejemplo, si hay 4 manzanas y 2 naranjas, la razón entre manzanas y naranjas es:
Razón = 4/2 = 2
Esto significa que hay 2 manzanas por cada 1 naranja.
Formas de Expresar una Razón
Como fracción: a/b
Con dos puntos: a:b
En palabras: «a es a b»
Ejemplo:
Si hay 6 niños y 3 niñas, la razón entre niños y niñas puede escribirse como:
6/3
6:3
En palabras: «6 es a 3»
Todas equivalen a la razón 2:1.
Proporcionalidad: Relación entre Razones Iguales
En matemáticas, la proporcionalidad es la relación entre dos razones que son iguales o constantes. Es una forma de comparar cantidades que crecen o disminuyen al mismo ritmo.
Tipos de Proporcionalidad
1. Proporcionalidad Directa
Dos cantidades son directamente proporcionales cuando al aumentar una, la otra también aumenta en la misma proporción (o al disminuir una, la otra también disminuye).
Ejemplo:
Si 1 lápiz cuesta $2, entonces 3 lápices cuestan $6.
La relación es:
2/1 = 6/3
Es proporcional porque la razón es constante.
2. Proporcionalidad Inversa
Dos cantidades son inversamente proporcionales cuando al aumentar una, la otra disminuye, de modo que el producto entre ellas se mantiene constante.
Ejemplo:
Si un trabajo se hace en 4 horas con 3 personas, ¿cuánto tardarían 6 personas?
Horas × Personas = 4 × 3 = 12
Entonces, con 6 personas:
Horas = 12/6 = 2
Más personas → menos tiempo → proporcionalidad inversa.
¿Qué es una Proporción?
Una proporción es una igualdad entre dos razones.
Ejemplo:
2/3 = 4/6
Esto significa que 2 es a 3 como 4 es a 6.
Aplicaciones de la Proporcionalidad
Resolver problemas de escalas (mapas, planos)
Convertir unidades (como km a metros)
Calcular porcentajes
Resolver reglas de tres
Regla de Tres: Método para Resolver Proporcionalidad
La regla de tres es un método sencillo y rápido que se usa en matemáticas para resolver problemas de proporcionalidad, es decir, cuando hay una relación constante entre cantidades.
Función de la Regla de Tres
Permite encontrar un valor desconocido cuando se conocen tres valores que guardan una relación proporcional.
Tipos de Regla de Tres
1. Regla de Tres Directa
Se usa cuando al aumentar una cantidad, la otra también aumenta (o ambas disminuyen).
Ejemplo típico: más horas trabajadas → más dinero ganado.
Ejemplo:
Si 4 cuadernos cuestan $12, ¿cuánto cuestan 6 cuadernos?
Resolvemos con una multiplicación cruzada:
Respuesta: $18
2. Regla de Tres Inversa
Se usa cuando al aumentar una cantidad, la otra disminuye.
Ejemplo: más personas trabajando → menos tiempo requerido.
Ejemplo:
Si 3 obreros hacen un trabajo en 6 días, ¿cuántos días tardan 6 obreros?
Respuesta: 3 días
Aplicaciones de la Regla de Tres
Calcular precios
Escalas o planos
Tiempo y velocidad
Recetas y mezclas
Problemas cotidianos con la estructura «si tanto cuesta/tarda/hace, ¿cuánto será para…?»
Representación Gráfica de la Proporcionalidad
Para representar la proporcionalidad gráficamente, se utilizan ejes cartesianos (X e Y). El tipo de gráfica resultante dependerá de si la relación es de proporcionalidad directa o inversa.
1. Gráfica de Proporcionalidad Directa
Cuando dos cantidades aumentan o disminuyen al mismo ritmo.
Características Clave:
La gráfica es una línea recta que pasa por el origen (0,0).
La fórmula es:
Y = KX
donde k es la constante de proporcionalidad.
Ejemplo:
Si 1 cuaderno cuesta $5, entonces 2 cuadernos cuestan $10, 3 cuestan $15, etc.
Tabla de valores:
| Cuadernos (x) | Precio (y) |
|---|---|
| 0 | 0 |
| 1 | 5 |
| 2 | 10 |
| 3 | 15 |
Gráfica:
Una línea recta que sube desde el punto (0,0), con pendiente constante.
2. Gráfica de Proporcionalidad Inversa
Cuando una cantidad aumenta y la otra disminuye, y el producto entre ambas es constante.
Características Clave:
La gráfica es una curva (hipérbola).
La fórmula es:
y = k/x
Ejemplo:
4 obreros hacen un trabajo en 6 días → Si aumentamos obreros, bajan los días.
Tabla de valores (k = 24):
| Obreros (x) | Días (y) |
|---|---|
| 2 | 12 |
| 3 | 8 |
| 4 | 6 |
| 6 | 4 |
| 8 | 3 |
Gráfica:
Una curva descendente, que nunca toca el eje X ni el eje Y (ya que el tiempo y el número de personas nunca pueden ser cero).
Conclusión
| Tipo de proporcionalidad | Gráfica | Relación | Ejemplo común |
|---|---|---|---|
| Directa | Línea recta desde (0,0) | y = kx | Precio por cantidad |
| Inversa | Curva (hipérbola) | y = k/x | Tiempo vs personas |
