Impulso y Cantidad de Movimiento
Impulso
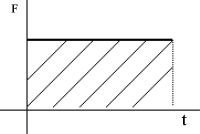
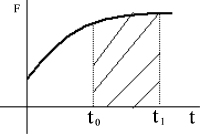
El impulso es el producto entre una fuerza y el tiempo durante el cual esta es aplicada. Es una magnitud vectorial. El módulo del impulso se representa como el área bajo la curva de la fuerza en el tiempo. Por lo tanto, si la fuerza es constante, el impulso se calcula multiplicando la Fuerza (F) por el intervalo de tiempo (Δt), mientras que, si la fuerza no es constante, se calcula integrando la fuerza entre los instantes de tiempo para los cuales se quiera conocer el impulso.
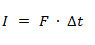
Donde:
- I = Impulso [kg·m/s]
- F = Fuerza [N]
- Δt = Intervalo de tiempo [s]
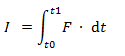
Donde:
- I = Impulso [kg·m/s]
- F = Fuerza [N]
- t0, t1 = Intervalo de tiempo [s]
Unidad de Impulso
El impulso se mide en kg·m/s, una unidad equivalente a N·s (Newton por segundo).
Cantidad de Movimiento
La cantidad de movimiento o momento lineal es el producto de la masa por la velocidad. La velocidad es un vector, mientras que la masa es un escalar. Como resultado, se obtiene un vector con la misma dirección y sentido que la velocidad.
La cantidad de movimiento sirve, por ejemplo, para diferenciar dos cuerpos que tengan la misma velocidad, pero distinta masa. El de mayor masa, a la misma velocidad, tendrá mayor cantidad de movimiento.
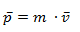
Donde:
- p = Cantidad de movimiento [kg·m/s]
- m = Masa [kg]
- v = Velocidad [m/s]
Unidad de Cantidad de Movimiento
La cantidad de movimiento se mide en kgċm/s. Tiene la misma unidad que el impulso, si bien son conceptos diferentes.
Relación entre Impulso y Cantidad de Movimiento
El impulso aplicado a un cuerpo es igual a la variación de la cantidad de movimiento. Por lo tanto, el impulso también puede calcularse como:
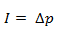
Dado que el impulso es igual a la fuerza por el tiempo, una fuerza aplicada durante un tiempo provoca una determinada variación en la cantidad de movimiento, independientemente de su masa:
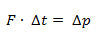
¿Qué relación existe entre el impulso y la cantidad de movimiento? (Preguntas y Respuestas)
A continuación, se presentan algunas respuestas y explicaciones recopiladas sobre este tema (fuente original: Yahoo Answers).
Respuesta Destacada
 xyzw1000 (hace 1 década)
xyzw1000 (hace 1 década)
Voy a discrepar un poco con las respuestas anteriores y muchas otras que, tal vez por abuso del lenguaje, no enuncian la propiedad tal como se debe, y quizás por desconocimiento histórico pretenden deducir la propiedad del impulso a partir de la Segunda Ley de Newton.
En realidad, se debe describir como la relación que existe entre el impulso y la VARIACIÓN DE LA CANTIDAD DE MOVIMIENTO.
He aquí el enunciado propuesto por Newton:
2.°) Principio Fundamental de la Dinámica de Traslación:
«El cambio de movimiento (cantidad de movimiento) es proporcional a la fuerza motriz que se le ha impreso, y sigue en la dirección de la línea recta en que se le imprimió la fuerza. O lo que es lo mismo, la fuerza que actúa sobre un cuerpo es igual a la derivada, respecto al tiempo, de su momento lineal.»
Se puede constatar en la siguiente dirección, leer completo el artículo:
http://fisica.laguia2000.com/dinamica-clasica/leyes-de-newton/principio-fundamental-de-la-dinamica-de-traslacion-segunda-ley-de-newtonOtras direcciones interesantes:
http://web.frm.utn.edu.ar/hciencia/fisica.htm
http://www.educared.net/concurso2001/322/historia.htm#3Yo diría lo siguiente: Cuando una masa experimenta una variación en su cantidad de movimiento (Newton decía momento lineal o moméntum) es porque sobre él actuó una fuerza durante cierto tiempo (impulso).
De allí aparece la expresión matemática:
Impulso = Variación de la cantidad de movimiento
Fuerza × tiempo = masa × variación de velocidad
Esa es la relación que pides.
Afectuosos saludos.
Otras Respuestas
 ? (hace 3 años)
? (hace 3 años)El impulso es igual al cambio en la cantidad de movimiento del cuerpo sobre el que actúa. En forma de ecuación, sería: FΔt = Δ(mv)
 Baster (hace 1 década)
Baster (hace 1 década)Cantidad de Movimiento (p):
==> «El producto de la masa de un cuerpo por su velocidad»
==> p = mvCuando la velocidad de un cuerpo varía, entonces hablamos de variación en la cantidad de movimiento:
==> Δp = m · Δv, si esta se realiza en un Δt, obtenemos:==> Δp/Δt = m · Δv/Δt,
lo cual representa una fuerza, ya que es el producto de una masa por la aceleración.==> F = m · Δv/Δt, por lo que:
==> F · Δt = m · Δv = I (impulso)Interpretación de Impulso:
==> Es el producto de una fuerza por la cantidad de tiempo (normalmente muy poco tiempo) que dura esa fuerza aplicada, o
==> Es el producto de la masa de un cuerpo por la variación de velocidad que experimenta el cuerpo.Conclusión:
Para que haya cantidad de movimiento, el objeto debe tener una velocidad; cuando esa velocidad varía en un tiempo normalmente muy breve, aparece el impulso.Impulso = Cambio en la Cantidad de movimiento.
Se desprende de la Segunda Ley de Newton:
F = m × a = m × (vf – vi) / Δt = (m vf – m vi) / ΔtSi pasamos el tiempo (Δt) a multiplicar a la izquierda, nos da:
F × Δt = m vf – m vi = cambio en la cantidad de movimiento.Donde:
vi = Velocidad inicial
vf = Velocidad final.→ La cantidad de movimiento se mide en kg·m/s. El impulso se mide en Newtons-segundo (N·s).
Si impulso un auto (aplico una fuerza durante un tiempo), le provoco un cambio en su cantidad de movimiento (m vf – m vi).
Estudiar esta materia implica que los alumnos logren los siguientes objetivos:
- Comprender el significado físico de momento lineal o cantidad de movimiento como medida de la capacidad de un cuerpo de actuar sobre otros en choques (movimientos unidimensionales).
- Comprender la relación entre impulso (de una fuerza constante) y momento lineal, así como el principio de conservación del momento lineal de un sistema en ausencia de un impulso externo neto.
- Comprender la noción de choque elástico e inelástico.
- Aplicar la conservación del momento lineal al cálculo de velocidades o masas de partículas que chocan entre sí en choques elásticos e inelásticos unidimensionales.
- Comprender cualitativamente los cambios de dirección que se producen en choques no frontales.
 |
¿Qué es el momento lineal?
Siempre que hablamos de movimiento nos referimos a los conceptos de posición, velocidad y aceleración para describirlo. Y cuando nos referimos a interacciones entre cuerpos, siempre hablamos de fuerzas.
En forma natural, estos dos hechos físicos, el movimiento de un cuerpo y las fuerzas que actúan sobre él, se relacionan.
Todos sabemos que un cuerpo en movimiento tiene la capacidad de ejercer una fuerza sobre otro que se encuentre en su camino. Llamaremos momento lineal o cantidad de movimiento (también conocido como moméntum) a la magnitud que nos permite medir esta capacidad.
Fue el propio Newton quien introdujo el concepto de momento lineal (aunque él lo llamaba cantidad de movimiento), que combina las magnitudes características de una partícula material en movimiento: su masa (toda partícula material tiene masa) y su velocidad (magnitud que caracteriza el movimiento).
La idea intuitiva tras esta definición está en que la «cantidad de movimiento» (el momento lineal o moméntum) dependía tanto de la masa como de la velocidad: si podemos imaginar una mosca y un camión, ambos moviéndose a 40 km/h, la experiencia cotidiana dice que la mosca se puede detener con la mano, mientras que el camión no, aunque los dos vayan a la misma velocidad.
Esta intuición llevó a definir una magnitud que fuera proporcional tanto a la masa del objeto móvil como a su velocidad.
¿Por qué es más difícil detener a un camión que a una mosca si se mueven a la misma velocidad? ¿Qué ocurre cuando chocan dos bolas de billar? ¿Qué pasa cuando la raqueta golpea la pelota de tenis?
 |
| El momento lineal es una magnitud que asocia la masa con la velocidad. |
Al golpear una pelota con una raqueta, un palo de golf o un bate de béisbol, la pelota experimenta un cambio muy grande en su velocidad en un tiempo muy pequeño.
Todos estos hechos tienen en común la magnitud cantidad de movimiento o momento lineal. Como ya lo dijimos, esta magnitud combina la inercia y el movimiento, o, lo que es lo mismo, la masa y la velocidad.
Un cuerpo puede tener una gran cantidad de movimiento (momento lineal) si tiene una masa muy grande o si se mueve a gran velocidad.
Matemáticamente, el momento lineal (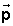 ) se define como:
) se define como: 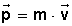
Por tanto, el momento lineal (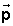 ) es una magnitud vectorial (kg·m/s), ya que resulta de multiplicar un escalar (la masa en kg) por un vector (la velocidad, en m/s). Su dirección y sentido coinciden con los del vector velocidad.
) es una magnitud vectorial (kg·m/s), ya que resulta de multiplicar un escalar (la masa en kg) por un vector (la velocidad, en m/s). Su dirección y sentido coinciden con los del vector velocidad.
Veamos un ejemplo sencillo:
Una persona de 64 kg camina por el parque con una velocidad de 2 m/s. ¿Cuál es la cantidad de movimiento de dicha persona?
Aplicamos la fórmula y reemplazamos los valores:
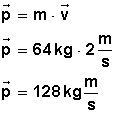
El momento lineal o la cantidad de movimiento de esta persona es 128 kg·m/s.
¿De qué depende el momento lineal?
Como dato previo, antes de continuar, no se debe confundir el concepto de momento lineal con otro concepto básico de la mecánica newtoniana, denominado momento angular, que es una magnitud diferente.
 |
| La bola espera recibir un impulso. |
Ahora trataremos de investigar de qué depende la magnitud vectorial definida como momento lineal.
En la imagen anterior vemos unas bolas de billar, las cuales, durante un juego, chocarán entre sí y con la banda de la mesa. En todos los casos supondremos que el choque dura una décima de segundo.
Impulso mecánico
Para que una bola de billar posea momento lineal, hay que proporcionárselo de alguna forma. Si observamos a un jugador de billar, resulta evidente que el momento lineal que adquiere la bola depende del golpe que se le da con el taco.
También observamos que ese momento lineal varía después de un choque con otra bola o con la banda de la mesa.
La magnitud que mide la variación del momento lineal de una partícula, y de la cual depende, se llama impulso.
¿Qué es el impulso?
Todos hemos visto cómo acelera un auto de Fórmula 1. Si mantiene esa acción (fuerza) durante más tiempo, adquiere mayor velocidad y puede ubicarse primero en la carrera.
Con esto nos damos cuenta de que el efecto que produce una fuerza que actúa sobre un cuerpo depende del tiempo que está actuando. Para medir este efecto se define la magnitud impulso mecánico.
El impulso mecánico (I) se define como el producto de la fuerza (F) por el intervalo de tiempo (Δt) durante el que ésta actúa:
Su formulación matemática es:
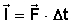
En forma descriptiva, diremos que el impulso es una magnitud vectorial que tiene la dirección y el sentido de la fuerza que lo produce. Su unidad en el Sistema Internacional (S.I.) es el N·s (Newton por segundo).
Si queremos comunicar un gran impulso a un cuerpo debemos aplicar una fuerza muy grande durante el mayor tiempo posible.
Las fuerzas aplicadas pueden variar con el tiempo; por eso se habla de fuerza media de impacto cuando golpeamos una pelota con una raqueta o con un palo de golf.
Ejercicio
Un palo de golf impacta en una bola con una fuerza media de 2000 N. Si el tiempo de contacto entre el palo y la bola es de 0,001 s, ¿cuál es el impulso que comunica a la bola?
La respuesta es: 2 N·s
 |
| Un sistema de partículas (bolas de billar). |
Conservación del momento lineal
Hasta ahora hemos hablado de momento lineal analizando el impacto solo de un cuerpo (bola de billar o partícula) sobre otro.
Ampliemos el concepto al choque de varias partículas (o bolas de billar), en lo que llamaremos un sistema de partículas.
Para ilustrar el concepto, pensemos en una mesa de billar, donde puede haber varias bolas moviéndose a la vez (las bolas representan partículas).
Entonces, llamaremos momento lineal de un sistema de varias partículas (varias bolas de billar, según nuestro ejemplo) a la suma vectorial de los momentos lineales de todas ellas.
Debemos notar que, como el momento lineal es un vector, cuando sumamos varios momentos tenemos que hacerlo como vectores, no como simples números.
Cuando algunas de las bolas chocan, sus momentos individuales se alteran: algunas se frenarán, otras se acelerarán…
Conclusiones sobre el momento lineal e impulso
Llamamos momento lineal a la magnitud que nos mide la capacidad que tiene un cuerpo de producir un efecto sobre otro en una colisión.
Llamamos impulso a la variación del momento lineal. Cuando aumentamos el momento lineal de un cuerpo, está recibiendo impulso positivo; cuando disminuimos ese mismo momento lineal, el impulso es negativo.
Principio de conservación del momento lineal: Cuando un sistema de partículas no recibe un impulso neto del exterior, su momento lineal total es constante.
Choques elásticos
Cuando dos cuerpos chocan puede que parte de la energía que llevan se utilice en deformarlos o bien se disipe en forma de calor, o puede que esta pérdida sea despreciable.
Si en un choque se conserva la energía cinética total de las partículas, el choque se considera elástico.
En este caso, la conservación del momento lineal y de la energía cinética determinan totalmente la velocidad de cada partícula tras el choque.
Tras el choque ambas seguirán moviéndose con distinta velocidad (al menos en el sentido); sin embargo, la suma de sus momentos lineales ha de permanecer constante.
 |
| El choque de las bolas de billar es elástico. Durante un choque elástico se conservan el momento lineal y la energía cinetica. |
Para ver una animación de un choque elástico ir a:
http://acer.forestales.upm.es/basicas/udfisica/asignaturas/fisica/dinamsist/colisiones.html
Choque inelástico
En el caso de que dos partículas choquen y sigan moviéndose juntas, se produce un choque perfectamente inelástico. Entonces también se conservará el momento lineal del conjunto.
 |
| Una desgracia «absolutamente inelástica». |
Choques absolutamente inelásticos
Un choque es absolutamente inelástico (o perfectamente inelástico) cuando se produce la mayor pérdida de energía cinética posible, compatible con la conservación del momento lineal total.
En el caso de choques frontales, esto supone que ambas partículas quedan adheridas una a otra.
Al contrario que en el caso del choque elástico, existen numerosos casos de choques absolutamente inelásticos.
Esto es lo que sucede, por ejemplo, cuando un automóvil choca contra un obstáculo fijo.
El móvil se deforma, por lo que las fuerzas internas hacen trabajo y el choque es inelástico. La energía cinética disminuye.
Conclusiones sobre el estudio de los choques entre partículas
Existen dos casos ideales en los que es posible determinar totalmente cómo se va a mover cada partícula (cada bola de billar, según nuestro ejemplo anterior) después de un choque:
- El choque frontal elástico, donde se conservan tanto la energía cinética como el momento lineal.
- El choque frontal absolutamente inelástico, donde ambas partículas permanecen unidas tras el choque. En este caso se produce la mayor pérdida de energía cinética posible.
Volver a Concepto de fuerza
Fuentes de Internet:
- http://www.educaplus.org/momentolineal/cantidad_movimiento.html
- http://newton.cnice.mec.es/materiales_didacticos/momento/momento-objetivos.htm
- http://recursostic.educacion.es/newton/web/materiales_didacticos/momento/aulamomento.pdf
- http://fisicayquimicaenflash.es/dinamica/dinamica01b.htm
- http://e-ducativa.catedu.es/44700165/aula/archivos/repositorio/1000/1152/html/index.html
- http://fisicaymasfisik.blogspot.com/2011/04/momentum-lineal.html
- http://conceptosdefisica.blogspot.com/2011/09/momento-lineal-cantidad-de-movimiento.html

 Ramiro de Costa Rica
Ramiro de Costa Rica