QUE ES LA FISICA
es la ciencia natural que estudia las propiedades y el comportamiento de la energía y la materia (como también cualquier cambio en ella que no altere la naturaleza de la misma), así como al tiempo, el espacio y las interacciones de estos cuatro conceptos entre sí.
La física es una de las más antiguas disciplinas académicas, tal vez la más antigua, ya que la astronomía es una de sus disciplinas. En los últimos dos milenios, la física fue considerada dentro de lo que ahora llamamos filosofía, química, y ciertas ramas de la matemática y la biología, pero durante la Revolución Científica en el siglo XVII surgió para convertirse en una ciencia moderna, única por derecho propio. Sin embargo, en algunas esferas como la física matemática y la química cuántica, los límites de la física siguen siendo difíciles de distinguir.
http://es.wikipedia.org/wiki/F%C3%ADsica
FENOMENO
es el aspecto que las cosas ofrecen ante nuestros sentidos; es decir, el primer contacto que tenemos con las cosas, lo que denominamos experiencia. La misma palabra hace pensar que detrás del fenómeno puede existir una estructura no perceptible directamente, el filósofo Immanuel Kant lo llamó noúmeno.
http://es.wikipedia.org/wiki/Fen%C3%B3meno
UNIDADES
es una cantidad estandarizada de una determinada magnitud física, definida y adoptada por convención o por ley.1 Cualquier valor de una cantidad física puede expresarse como un múltiplo de la unidad de medida.
En general, una unidad de medida toma su valor a partir de un patrón o de una composición de otras unidades definidas previamente. Las primeras unidades se conocen como unidades básicas o de base (fundamentales), mientras que las segundas se llaman unidades derivadas.2
Un conjunto de unidades de medida en el que ninguna magnitud tenga más de una unidad asociada es denominado sistema de unidades.3
Todas las unidades denotan cantidades escalares. En el caso de las magnitudes vectoriales, se interpreta que cada uno de los componentes está expresado en la unidad indicada.1
http://es.wikipedia.org/wiki/Unidad_de_medida
MAGNITUDES
Una magnitud física es una propiedad o cualidad medible de un sistema físico, es decir, a la que se le pueden asignar distintos valores como resultado de una medición o una relación de medidas. Las magnitudes físicas se miden usando un patrón que tenga bien definida esa magnitud, y tomando como unidad la cantidad de esa propiedad que posea el objeto patrón. Por ejemplo, se considera que el patrón principal de longitud es el metro en el Sistema Internacional de Unidades.
http://es.wikipedia.org/wiki/Magnitud_f%C3%ADsica
SISTEMA DE UNIDADES
Un sistema de unidades es un conjunto que consiste en unidades de medida. Definen un conjunto básico de unidades de medida a partir del cual se derivan el resto. Existen varios sistemas de unidades:
- Sistema Internacional de Unidades o SI:
Es el sistema más usado. Sus unidades básicas son: el metro, el kilogramo, el segundo, el amperio, el kelvin, la candela y el mol. Las demás unidades son derivadas del Sistema Internacional. Sistema Métrico Decimal
Primer sistema unificado de medidas.- Sistema Cegesimal o CGS:
Denominado así porque sus unidades básicas son el centímetro, el gramo y el segundo. Sistema Natural
En el cual las unidades se escogen de forma que ciertas constantes físicas valgan exactamente 1.Sistema Técnico de Unidades
Derivado del sistema métrico con unidades del anterior. Este sistema está en desuso.Sistema Métrico Legal Argentino
Sistema de medidas,unidades y magnitudes que se utiliza en Argentina.Sistema anglosajón de unidades
Aún utilizado en algunos países anglosajones. Muchos de ellos lo están reemplazando por el Sistema Internacional de Unidades.
Además de éstos, existen unidades prácticas usadas en diferentes campos y ciencias. Algunas de ellas son:
- Unidades atómicas
- Unidades usadas en Astronomía
- Unidades de longitud
- Unidades de superficie
- Unidades de volumen
- Unidades de masa
- Unidades de medida de energía
- Unidades de temperatura
- Unidades de densidad
http://es.wikipedia.org/wiki/Sistema_de_unidades
FACTOR DE CONVERCION
El factor de conversión o de unidad es una fracción en la que el numerador y el denominador son cantidades iguales expresadas en unidades de medida distintas, de tal manera, que esta fracción equivale a la unidad. Método efectivo para cambio de unidades y resolución de ejercicios sencillos dejando de utilizar la regla de tres. Cada factor de conversión se construye con una equivalencia (igualdad entre dos cantidades).
- Ejemplo 1: pasar 15 pulgadas a centímetros (equivalencia: 1 pulgada = 2,54 cm )
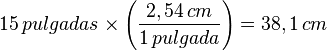
- el factor unitario :
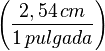 se construye a partir de la equivalencia dada.
se construye a partir de la equivalencia dada.
- Ejemplo 2: pasar 25 metros por segundo a kilómetros por hora (equivalencias: 1 kilómetro = 1000 metros, 1 hora = 3600 segundos)
- Ejemplo 3: obtener la masa de 10 litros de mercurio (densidad del mercurio: 13,6 kilogramos por decímetro cúbico)
- Nótese que un litro es lo mismo que un decímetro cúbico.

- En cada una de las fracciones entre paréntesis se ha empleado la misma medida en unidades distintas de forma que al final sólo quedaba la unidad que se pedía
http://es.wikipedia.org/wiki/Factor_de_conversi%C3%B3n
VECTORES
En física, un vector (también llamado vector euclidiano o vector geométrico) es una magnitud física definida por un punto del espacio donde se mide dicha magnitud, además de un módulo (o longitud), su dirección (u orientación) y su sentido (que distingue el origen del extremo).123
En Matemáticas se define un vector como un elemento de un espacio vectorial, esta noción es más abstracta y para muchos espacios vectoriales no es posible representar sus vectores mediante el módulo, la longitud y la orientación. En particular los espacios de dimensión infinita sin producto escalar no son representables de ese modo. Los vectores en un espacio euclídeo se pueden representar geométricamente como segmentos de recta dirigidos («flechas») en el plano  o en el espacio
o en el espacio  .
.
Algunos ejemplos de magnitudes físicas que son magnitudes vectoriales: la velocidad con que se desplaza un móvil, ya que no queda definida tan sólo por su módulo (lo que marca el velocímetro, en el caso de un automóvil), sino que se requiere indicar la dirección y el sentido (hacia donde se dirige); la fuerza que actúa sobre un objeto, ya que su efecto depende, además de su intensidad o módulo, de la dirección en la que actúa; también, el desplazamiento de un objeto.
TIPOS
Según los criterios que se utilicen para determinar la igualdad o equipolencia de dos vectores, pueden distinguirse distintos tipos de los mismos:
- Vectores libres: no están aplicados en ningún punto en particular.
- Vectores deslizantes: su punto de aplicación puede deslizar a lo largo de su recta de acción.
- Vectores fijos o ligados: están aplicados en un punto en particular.
Podemos referirnos también a:
- Vectores unitarios: vectores de módulo unidad.
- Vectores concurrentes o angulares: son aquellas cuyas direcciones o líneas de acción pasan por un mismo punto. También se les suele llamar angulares por que forman un ángulo entre ellas.
Vectores opuestos
Vectores de igual magnitud y dirección, pero sentidos contrarios.1 En inglés se dice que son de igual magnitud pero direcciones contrarias, ya que la dirección también indica el sentido.Vectores colineales
Los vectores que comparten una misma recta de acción.- Vectores paralelos: si sobre un cuerpo rígido actúan dos o más fuerzas cuyas líneas de acción son paralelas.
- Vectores coplanarios: los vectores cuyas rectas de acción son coplanarias (situadas en un mismo plano).
http://es.wikipedia.org/wiki/Vector_%28f%C3%ADsica%29#Clasificaci.C3.B3n_de_vectores
MÉTODOS GRÁFICOS PARA EL CÁLCULO DE LOS VECTORES RESULTANTE V R Y EQUILIBRANTE V E .
Introducción:
Antes de entrar a la aplicación de los métodos gráficos es necesario tener en cuenta las siguientes consideraciones.
Para la «y» + arriba y – abajo.
Escala = Magnitud del vector x de referencia / Magnitud en cm. que se desea que tenga en el papel, o seaEsc. = Vx / cm. De Vx .
por ejemplo si tenemos un vector A = 120 Km/h a 30° al norte del esteLa escala será:
Ejemplo
Metodo del triangulo
Figura 1
En la figura 1 el vector de color negro es la suma vectorial de los vectores de color rojo y de color azul
En el caso de la figura 1 las relaciones posibles entre los lados de ese triángulo son las siguientes:


metodo del poligono:


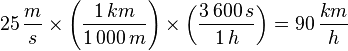
INTERESANTE INTERESANTE ME SIRVIO PARA MI TAREA